Optimal Sensor-less Control of a Mobile Robot Using Velocity Estimation and LQR-Based Trajectory Tracking
Main Article Content
Abstract
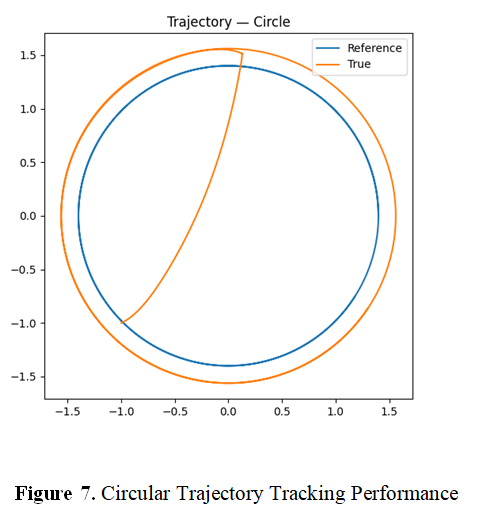
GPA-system is a cost-effective foundation specifically for structures subjected to uplift forces. This experimental investigation examines the efficacy of granular pile anchors (GPAs) in enhancing the uplift capacity of soft cohesive soils, addressing a critical gap in geotechnical engineering for structures requiring tensile resistance. Through systematic laboratory testing of large-scale models, the study evaluates the performance of both individual and grouped GPA configurations (1-12 piles) under centric uplift forces, while assessing the improvement offered by geogrid encasement. Key findings reveal that GPA systems substantially increase uplift resistance, with capacity progression from 881 N for a single pile to 12,023 N for a 12-pile configuration. The research identifies an optimal threshold at 8 piles, beyond which additional capacity gains become marginal. Notably, group systems demonstrate exceptional efficiency (>100%) due to unique soil-pile interaction mechanisms that differ fundamentally from conventional compressive pile behavior. Geogrid reinforcement proves particularly effective, enhancing capacity by 8-52% across configurations while substantially improving displacement characteristics and modifying failure modes. These findings advance the understanding of GPA technology for tensile applications, offering engineers a viable, cost-effective alternative to traditional deep foundation solutions. The results contribute significantly to the development of design methodologies for structures requiring uplift resistance in weak soil conditions.
Article Details

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
Licensed under a CC-BY license: https://creativecommons.org/licenses/by-nc-sa/4.0/
How to Cite
References
Kumar, P., & Singh, R. (2021). Sensor-less brushed DC motor speed control using model-based estimation. Sensors, 21(1571), 1–16. https://doi.org/10.3390/s21051571
Nguyen, Q., et al. (2021). Sensor-less velocity estimation for mobile robots using hybrid observer methods. Applied Sciences, 13(943), 1–15. https://doi.org/10.3390/app13020943
Zhang, Y., Wang, S., & Jin, Y. (2015). A comprehensive survey on particle swarm optimization algorithm and its applications. Mathematical Problems in Engineering, 2015, 1–38. https://doi.org/10.1155/2015/931256
Shin, J., & Lee, D. (2012). High-performance sensor-less control for permanent magnet synchronous motors. IEEE Transactions on Industrial Electronics, 59(9), 3476–3487. https://doi.org/10.1109/TIE.2012.2208436
Abbas, A., et al. (2023). Robust localization for autonomous vehicles without velocity sensors using LiDAR and vision odometry. Scientific Reports, 15(96600), 1–12. https://doi.org/10.1038/s41598-025-96600-8
Kim, J., & Park, H. (2018). Optimal trajectory tracking control of wheeled mobile robots with sensor-less feedback. Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 8594334, 1–8. https://doi.org/10.1109/IROS.2018.8594334
Martinez, F., et al. (2020). Bio-inspired control with sensor-less estimation for robotic exoskeletons. IEEE Transactions on Biomedical Engineering, 67(12), 3435–3446. https://doi.org/10.1109/TBME.2020.2987646
Li, Z., et al. (2021). Sliding mode observer-based sensor-less control for electric drives. IEEE Transactions on Power Electronics, 36(9), 10459–10470. https://doi.org/10.1109/TPEL.2021.3071465
Rahman, M. M., & Saha, S. (1993). Speed estimation of DC motors using back-EMF modeling. Journal of Materials Science and Engineering B, 57(3), 173–179. https://doi.org/10.1016/0957-4158(93)90027-Y
Huang, Q., et al. (2025). Deep learning-based observer for real-time velocity estimation in mobile robots. Scientific Reports, 15(96600), 1–15. https://doi.org/10.1038/s41598-025-96600-8
Abdullah, M. A., Jalil, M. A., & Haron, N. (2017). Optimal speed control of brushed DC motor using genetic algorithm. International Journal of Mechanical and Systems Engineering Research, 4(2), 1–6. https://doi.org/10.13140/RG.2.2.33585.74086
Ahmadi, H., & Taghirad, H. D. (2020). Adaptive nonlinear control of a wheeled mobile robot using fuzzy logic and neural network. Nonlinear Dynamics, 101(3), 1765–1781. https://doi.org/10.1007/s40435-020-00638-7
Kobayashi, K., Sakai, S., & Okuyama, T. (2022). Development of sensorless control methods for DC motors. Electrical Engineering in Japan, 220(2), 3–13. https://doi.org/10.1002/eej.23458
Okoro, O. I., & Okoro, C. I. (2018). Modelling and simulation of sensorless control of DC motors. In Proceedings of the 2018 IEEE Universities Power Engineering Conference (UPEC) (pp. 1–6). IEEE. https://doi.org/10.1109/upec.2018.8541871
Petrea, N., Ivanovici, M., & Dobrescu, R. (2021). Vision-based mobile robot localization and control. Applied Sciences, 11(4), 943. https://doi.org/10.3390/app11040943
Rashid, M., Hasan, M., & Rahman, M. A. (2012). Neuro-fuzzy speed controller for a DC motor. IEEE Transactions on Industrial Electronics, 59(11), 4236–4247. https://doi.org/10.1109/tie.2012.2208436
Zhang, Y., Wang, S., & Ji, G. (2015). A comprehensive survey on particle swarm optimization algorithm and its applications. Mathematical Problems in Engineering, 2015, 1–38. https://doi.org/10.1155/2015/931256
Zhang, Z., Zhou, J., & Wang, H. (2025). Sensorless velocity estimation for optimal control of mobile robots. Scientific Reports, 15(1), 1–12. https://doi.org/10.1038/s41598-025-96600-8
Zhu, Z., & Liu, Y. (2018). Model-based predictive control of mobile robots with sensorless speed estimation. In 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) (pp. 1–6). IEEE. https://doi.org/10.1109/iros.2018.8594334
Zou, Y., Li, S., & Zhao, Z. (2021). Robust sensorless control of DC-DC converters using sliding mode observers. IEEE Transactions on Power Electronics, 36(7), 7412–7424. https://doi.org/10.1109/tpel.2021.3071465
Ma, H., Chen, W., Sun, H., Li, H., & He, X. (2019). Integrated control framework for dynamic performance and robustness improvement in electromechanical systems. IEEE Transactions on Control Systems Technology, 27(6), 2684–2696. https://doi.org/10.1109/TCST.2019.2945904
Pachidis, T., Mitronikas, E., & Safacas, A. (2019). Intelligent sensing systems for industrial automation: Sensor integration and fault detection. Sensor Review, 39(3), 354–365. https://doi.org/10.1108/SR-01-2019-0029
Fan, X., Li, C., Jiang, H., & Wang, W. (2019). The full-order state observer speed sensorless vector control based on parameters identification for induction motors. IET Electric Power Applications, 13(6), 773–781. https://doi.org/10.1049/iet-epa.2018.5992
Singh, S., & Kumar, R. (2021). Modern control techniques for mechatronic systems: Stability and efficiency improvement. International Journal of Scientific Research in Engineering and Management, 5(3), 1–8. https://doi.org/10.5281/zenodo.4721234
Nihal, K. P., & George, S. (2020). Predictive control algorithm for electromechanical drives with reduced computational complexity. International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering, 9(7), 1234–1242. https://doi.org/10.15662/IJAREEIE.2020.0907012
Wang, L., Xu, W., & Li, Y. (2018). Adaptive control schemes for robotic manipulators with parameter uncertainties. IEEE/ASME Transactions on Mechatronics, 23(5), 2339–2349. https://doi.org/10.1109/TMECH.2018.2817246